
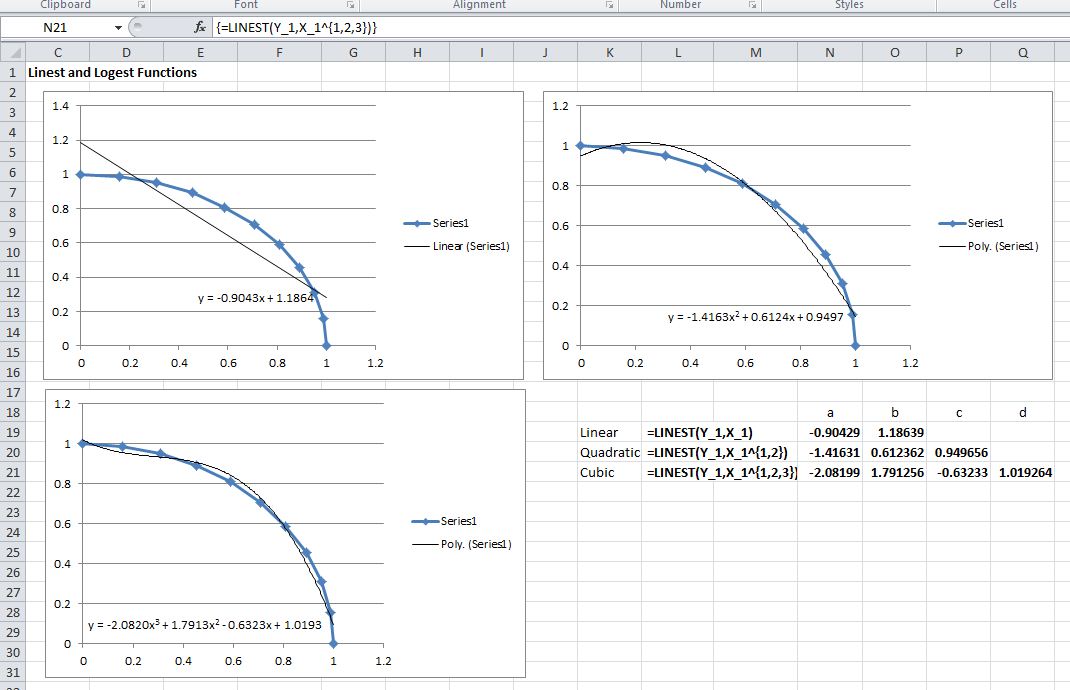
And I think if we go up to a third order third order actually fits perfectly because for a third order polynomial you need you need four constants 1234 And since we have four data points we can pick those for constant. And it's just, you know, I've said it nicely for us um and we can see that it goes does a really good job, although, you know, I think it's a little over on this point, a little under on this point. And then I showed the equation here and here's the equation and we can see that it has the same values that we have up here that basically used the same same functions to figure out what this polynomial is here. And if we go back here, we say we can have degrees too.
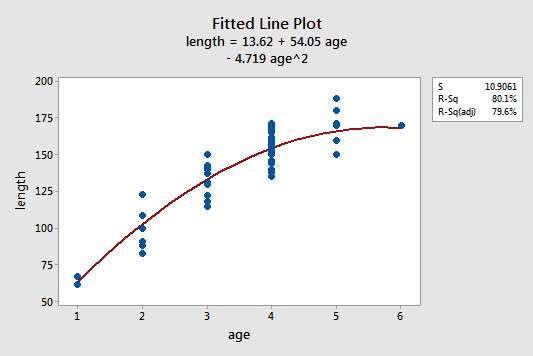
So we have the coefficient front of X squared is minus 1.25 In front of X is your 0.45 And in front of C or the constant C is nine point um 95 And so if we if we actually turn their trend line back on, let's see here where we got trend line, we want none but a polynomial. So here's the coefficients that we have for our quadratic fit. I talked about that in more detail and problem 24. So I used them this linear estimation function and and in numbers to figure out these coefficients. In fact it doesn't do very good because I also found the linear regression. It doesn't look like a line would do very good. Um you know, it looks like pretty parabolic.
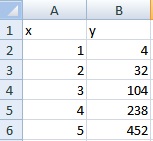
So you can see here that here's the no my problem. We'll see that, you know, they found nicely on a parabola here. So I just squared these and then we plot them. So to fit a quadratic, I need to make a column of X squared values. We have this whole thing here where I did are fitting and I used Apple's numbers for on an ipad here. We are given four data points, 0 10, 19 26 and 30 two.


 0 kommentar(er)
0 kommentar(er)
